| Asteroiden und Meteoriten | Mathematische und physikalische Grundlagen | Impressum und Kontakt |
Mathematische und physikalische Grundlagen
|
Häufigkeit der Meteoriden
Die Häufigkeit, mit der die Meteoriden auftreten, hängt von deren Größe ab. Sei dM die Größe des Meteoriden in Metern (genauer sein mittlerer Durchmesser), dann berechnet sich die Häufigkeit seines Auftretens empirisch zu: Häufigkeit [pro Jahr] = 218,8 / dM[m]2,68
Kinetische Energie eines Meteoriden
Bei hohen Energien mit über 1012 J = 1 Tera-Joule können folgende Vergleichsgrößen herangezogen werden:
Die Masse M des Meteoroiden in kg berechnet sich über sein Volumen und seiner Dichte. Sie beträgt: M [kg] = 1/6 * ρ * π * dM[m]3.
Daraus errechnet sich die kinetische Energie zu: EKin [J]
= ½ * M
*v2 =
1/12 * ρ * π * dM[m]3 * v2
Die Sprengkraft von 1 Kilo-Tonne TNT entspricht 4,185 * 1012J. = 2,511 * 1017 J
Dichte der Erdatmosphäre
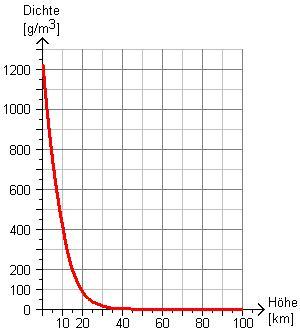
Die Dichte der Erdatmosphäre nimmt mit der Höhe exponentiell ab. Alle 5,5 km Höhenunterschied halbiert sich der Luftdruck. Für die Standardatmosphäre gilt eine Bodentemperatur von 15°C und 1013,25 hPa Luftdruck. Die Temperatur nimmt mit der Höhe um ca. 0,5 bis 1,0 °C pro 100 m Höhendifferenz ab. Für Höhen bis zu 11.000 m kann man die internationale Höhenformel verwenden: ρL [kg/m3 ]=1,2255 * (1 - 6,5 * Höhe [m] / 288000)4,255 * (1 + Höhe [m] / 5000000). Für größere Höhen müssen abschnittsweise andere Formeln verwendet werden.
|
|
Aus nebenstehendem Diagramm kann man entnehmen, wie sich die Dichte der Erdatmosphäre mit der Höhe verhält. |
|
|
Geschwindigkeitsänderung des Meteoroiden
In Abhängigkeit von der Höhe über dem Erdboden, der Größe des Meteoroiden und der Dichte der Erdatmosphäre erfährt der Meteoroid eine zusätzliche Beschleunigung durch die Schwerkraft der Erde und einen Abbremseffekt durch die Reibung in der Erdatmosphäre.
Mit dem Erdradius RE = 6378,4 km und der Erdbeschleunigung g0 = 9,80665 am Erdboden berechnet sich
die momentane Erdbeschleunigung g zu: g (Höhe) = g0 * RE2/ (RE + Höhe)2
Mit Hilfe des Widerstandsbeiwertes cw des Meteoroiden, seiner Geschwindigkeit v, seinem Querschnittsdurchmesser dQ und seiner
Masse M berechnet sich die momentane Bremsbeschleunigung aB des Meteoroiden zu:
aB = cw * π * dQ2 * ρL * v2 / (4 * M) Die momentane Gesamtbeschleunigung ist somit: a = g (Höhe) - aB.
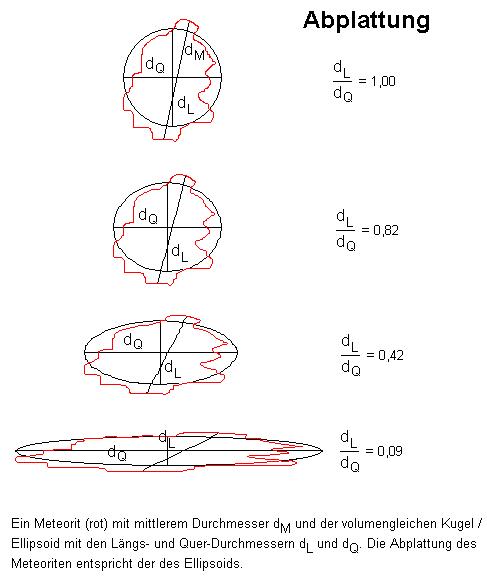
Abplattung
Beim Flug durch die Erdatmosphäre wird der Meteoroid aufgrund der starken Bremskräfte zunehmends deformiert.
In Bewegungsrichtung wird der Körper immer flacher, quer zur Beobachtungsrichtung dehnt er sich jedoch aus, wodurch sich die Querschnittsfläche bezüglich
der angreifenden Bremskraft erhöht und dadurch der Bremseffekt noch weiter verstärkt wird. Zu kleine Meteoriten verglühen bereits, bevor sie merklich
abgeplattet werden könnten; zu große Meteoriten schlagen auf, bevor sie eine merkliche Abbremsung erfahren. Mittelgroße Meteoroiden aber erfahren eine
rapide Abbremsung. Ungeheure Kräfte zerren an ihnen, nach einiger Zeit sind sie um ein Vielfaches abgeplattet als zu Beginn. Es wird eine
Stabilitätsgrenze erreicht, bei deren Überschreiten, der Meteoroid auseinanderfällt – er explodiert.
Sobald POF ≥ є ist, berechnet sich die Wachstumsrate der Querschnittsfläche zu Δŕw = POF /
(ρM * dQ). Δrz = ½ * Δŕw *
Δt² + Δŕw * Δt auf den Wert dQ= dQ (vorher)+ Δrz |
|
|
Dementsprechend verringert sich der Längs-
|
|
Helligkeiten
Tagseite der Erde in Erscheinung tritt. Je größer das Objekt ist und je näher er zum Beobachter ist,
desto heller erscheint er. 2) Durch die Reibung während seines Fluges durch die Erdatmosphäre ionisiert er die ihn umgebende Luft und regt sie zum Leuchten an. Auch hier gilt: Je größer das Objekt ist, je schneller es durch die
Atmosphäre fliegt und je dichter diese ist, desto heller erscheint er. Drückt man diese Helligkeiten in der astronomischen Magnitudenskala aus, ergibt sich die Reflektionshelligkeit
H1 zu: |
|
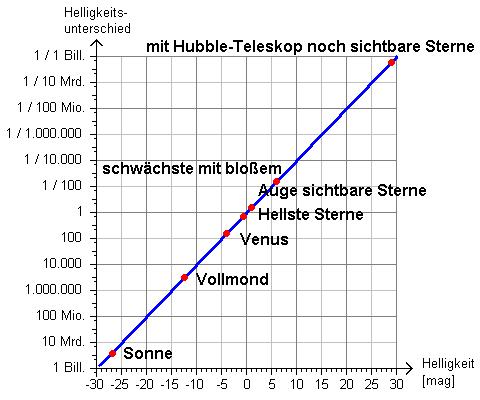
Rechts sehen Sie, über wie viele astronomische Größenklassen sich die Helligkeiten der Objekte am Himmel erstrecken. Beachten Sie die logarithmische Skala auf der nach oben weisenden Achse: Jedes Kästchen bedeutet hier eine Multiplizierung mit dem Faktor 100 ! |
|
|
Kratergrößen
Bei einem Einschlag in Felsgestein kann man bei den üblichen Geschwindigkeiten als Faustregel verwenden, dass der Durchmesser des Sekundärkraters etwa dem 20-fachen Objekt-Durchmesser (im Moment des Einschlags) entspricht.
Wa[m] = 0,88 * EKin[J]1/4.
Auf dem offenen Meer sind Tsunami-Wellen also viele hundert Stundenkilometer schnell, die
Wellenlänge ist kilometergroß und die Höhenamplitude meist relativ gering. Nähert sich die Welle den Küsten, wird die Wassertiefe immer flacher und die
Welle damit langsamer. Jedoch drängen von weiter draußen auf dem Meer die immer noch schnelleren Wellen nach, so dass sich die Wellenberge immer mehr
auftürmen, je näher sie der Küste kommen. Bei einer Meerestiefe von 5000 m ist die Tsunami-Welle 789 km/h schnell, bei 1000 m Meerestiefe nur noch
353 km/h und bei 10 m tiefem Wasser kurz vor der Küste gar nur noch 35 km/h. Die Welle ist gegenüber vorher etwa 20 mal langsamer, dafür aber auch
20 mal so hoch.
|
|